The Dzhanibekov Effect

Today something from the field of physics for the inquisitive: The Dzhanibekov effect, also known as the tennis racket theorem, explains an instability of rotating bodies with three different moments of inertia. The moment of inertia indicates the resistance of a body to changes in its rotational movement. It depends on the particular axis of rotation and the geometry. Understanding the dynamics of classical Hamiltonian systems is still a crucial goal with a multitude of applications that go far beyond their mathematical description. In the case of integrable systems with few degrees of freedom, an efficient approach is based on a geometric analysis to characterize the dynamic properties of the mechanical system. Such geometrical phenomena are typically the origin of the robustness of certain effects that can be observed experimentally. one of them is the so-called. Dzhanibekov effect or also called the tennis racket effect.

Janibekov effect in the weightlessness of the ISS

An excellent and detailed theoretical derivation of the phenomenon can be found here (https://arxiv.org/pdf/1606.08237.pdf). We are dealing here with one who is a little rougher, but who nevertheless explains the phenomenon. Unfortunately, some prior knowledge of the dynamics of rigid bodies is necessary here:

Consider a matrix of inertia (diagonalized) with moments of inertia I1 and I2 and I3 such that I1 is smallest and I3 is largest. Now consider the movement around the axis of the main moment of inertia I3. The angular velocity vector is:

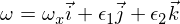
where the epsilons are small perturbations in the other two main axes. If you now insert this into the Euler equations, you get:

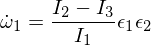
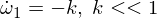
Now we differentiate the second Euler equation:

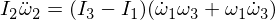
The substitution of omega 1 and omega 3 in our expression, and since multiplying the epsilons makes them small enough to ignore,

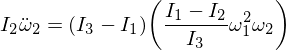
This gives us a differential equation for Omega 2 of the form:

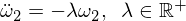
The basic solution is:

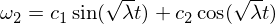
Hence we know that the rotational disorder in the omega-1 axis is stable and makes periodic movements, or in the terminology of rigid body movement, that it makes a precession. The disorder in omega 3 follows a similar argument as above, and I'll leave it as an exercise for you to work through it. For the intermediate axis we have:

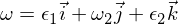
Inserted into the Euler equations:

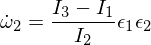
Differentiating the third Euler equation gives:

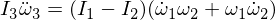
Let's replace our derived expressions:

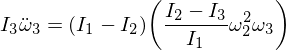
Now rearrange and derive the following differential equation:

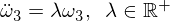
Notice that the coefficient is now positive, which therefore leads to exponential solutions:

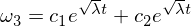
This solution shows that omega 3 is unstable along the intermediate axis with a disturbance of omega 2!

What does that mean?

Now we can combine everything that we have derived and learned to understand the theorem. Put simply: if the rotation along the intermediate axis is disturbed, a differential equation with exponential solutions results. This leads to an unstable movement, in contrast to the precise movement observed in the other two axes. This result is quite surprising. There is no intuitive support for such a theorem as we cannot imagine why the intermediate moment of inertia would result in an unstable rotation. It seems like it's purely mathematical in nature.