A "difficult" problem
Today something from the category "forgotten math". There are always very interesting algebraic number relationships that are unfortunately rarely or not at all in the curriculum, but which expand the understanding of numbers and mathematical intuition.
Let's say someone asks you to solve the next equation without any technical tools.
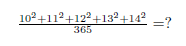
Can you do this?
Ok at first sight is not that easy. But when you know the special and interesting relationship between these numbers, it's really simple:
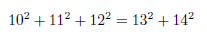
The left components of the equation are: 100 + 121 + 144 = 365; In other words:
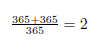
Ok, let's use simple algebra to find out if we can find more such sequences: The first number we are looking for is "x":
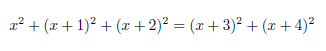
or simply:
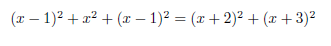
The equation can be written as a quadratic equation:
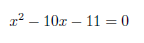
The solution is:
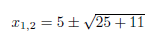
In fact, we have two solutions:
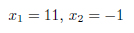
This means that we have two sequences of desired behaviors. The first one has already been checked by (10,11,12,13,14). The new one is:
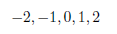
Let's check it out:
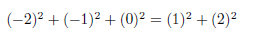
It works! A small simple example of the power and beauty of algebraic methods.